本文最后更新于：1 小时前

# 文法问题处理器

# 问题描述

设计一个文法规则处理器，使其能够实现以下功能：

检查并去除有害规则和多余规则
消除该文法的左公共因子
消除该文法的左递归
求出经过前面步骤处理好的文法各非终结符号的 first 集合与 follow 集合
对输入的句子进行最左推导分析
使用符号’@‘代表’ε’

# 系统流程图

系统流程图

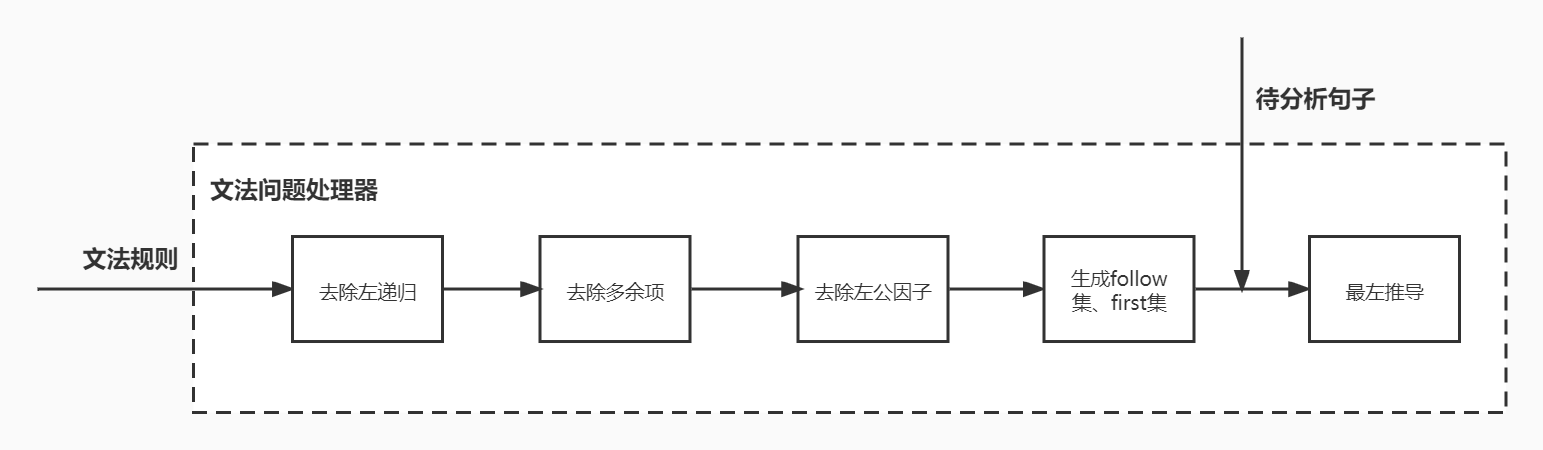
# 存储结构设计

# 文法规则存储结构

对于一条文法规则，使用 string 来存储左边部分，用 vector<vector<string>> 来存储右边部分。

例如：对于文法规则 A -> acd | efg | hig，则右边部分的存储结构为 [[a, c, d], [e, f, g], [h, i, g]]

类声明如下：

//使用'@'标识EPSILON
#define EPSILON "@"
class LinkNode
{
public:
    //规则左部
    string left;
    //规则右部分 abc | def | hji，一个vector<char>元素代表一种可能
    vector<vector<string>> right;
    //构造函数，str是左边部分
    LinkNode(string str);
    //右边添加规则
    void insert(vector<string> &nodes);
    //判断是否有epsilon存在
    bool includesEpsilon();
    //toString()方法
    string toString();
};

# 文法处理器存储结构

文法处理器的功能包括对文法的存储以及各种处理操作。

使用 vector<LinkNode> 存储多条文法规则
使用 vector<string> 存储用户输入的待推导句子、终结符号、非终结符号
使用 map<string, set<string>> 存储各个非终结符号对应的 first 集合和 follow 集合

类声明如下：

class Processor
{
public:
    vector<string>input;//存用户输入的待分析句子
    int startWordIndex;//开始节点索引    
    string startNode;//开始结点值   
    vector<LinkNode> grammers;//存文法   
    vector<string> finalWord;//终结符号
    vector<string> nonFinalWord;//非终结符号   
    map<string, set<string>> first;//First集合   
    map<string, set<string>> follow;//Follow集合   
    ofstream log;//文件流，用于写出日志   
    Processor(string filePath);//构造函数，参数是文件路径 
    void init();//初始化终结符号和非终结符号    
    void dealLeftRecursion();//处理左递归   
    void dealLeftCommonFacotr();//处理左公因子 
    void simplify();//化简 
    void getFirst();//生成First集合   
    void getFollow();//生成Follow集合   
    bool isFinalWord(string word);//判断是不是终结符号  
    bool isWord(string word);//判断是不是该文法能处理的符号
    //按照指定符号拆分字符串
    vector<string> splitString(string str, string spliter);  
    void printGrammers();//输出当前文法信息到log文件   
    vector<vector<string>> leftMostDerivation();//最左推导
private:
    //用于存储是否访问过
    bool visited[MAX_NODE_NUMBER];
    //找到非终结符号word对应的是第几条规则
    int getIndex(string word);
    //配合getFirst()函数使用，递归实现求某条规则的first集合
    void findFirst(int i);
    void dfs(int x);//深度优先遍历
    //处理单条文法的左公因子
    vector<LinkNode> dealCommonFactor(LinkNode&node);
    //生成一个没有使用过的非终结符号名
    string generateNewName(string source);
    //将str1的follow添加到str2的follow集合
    void append(const string &str1, const string &str2);
};

# 界面设计

# 读取文法并做处理的界面

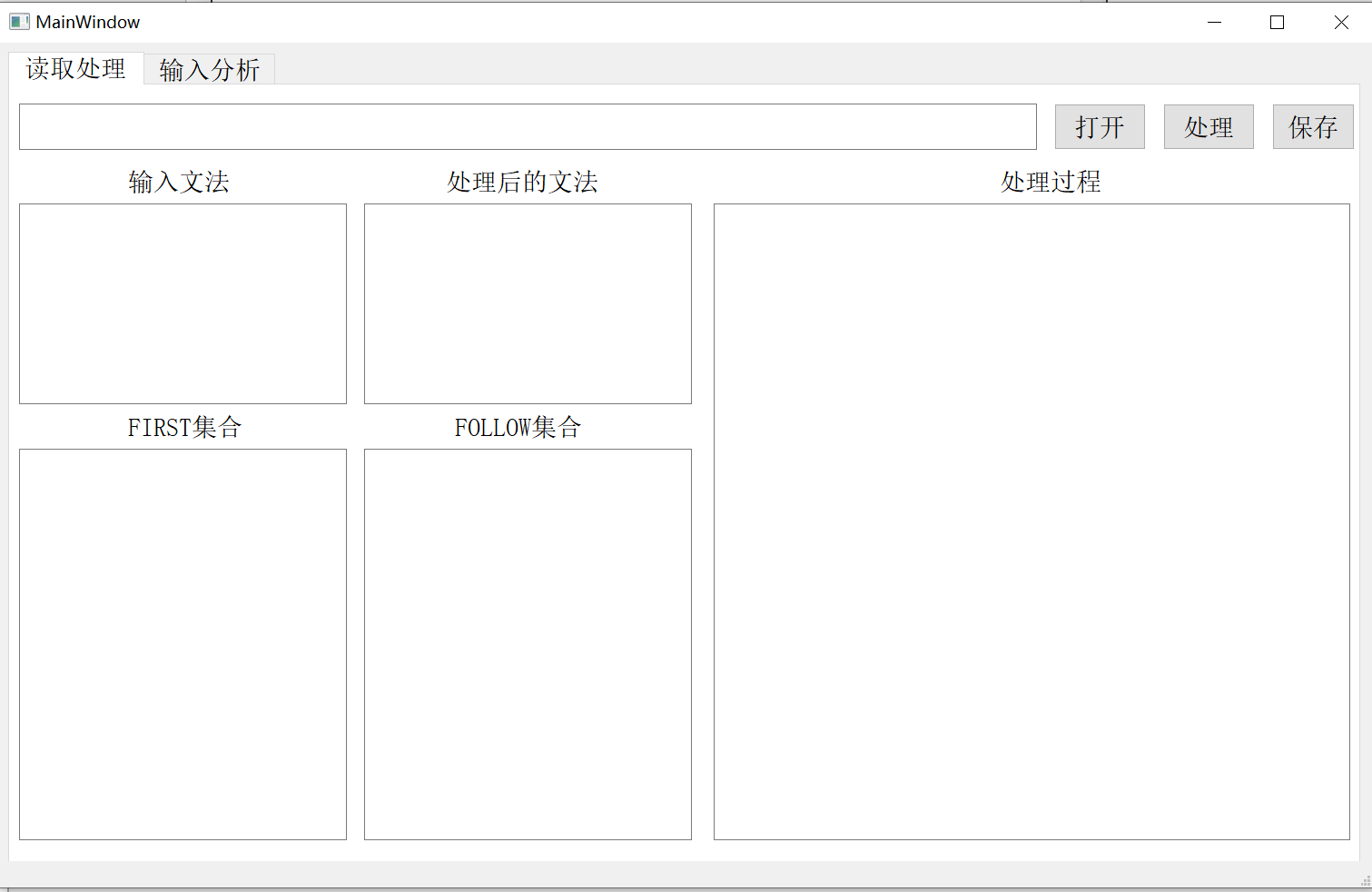
读取文法并做处理的界面

# 最左推导界面

最左推导界面

# 主要算法说明

# 去除无效文法

对于形如 A -> A 的有害规则，在读取规则时就可以将其去除
对于直接或间接无法终止的规则，暂时没想好怎么处理……
对于用不到的无效规则，可以采用深度优先的方法，设置一个 bool 数组用于标记是否访问过各条文法规则，从开始结点遍历文法规则，当遍历结束时，对于没有访问过的文法规则，就将其删除

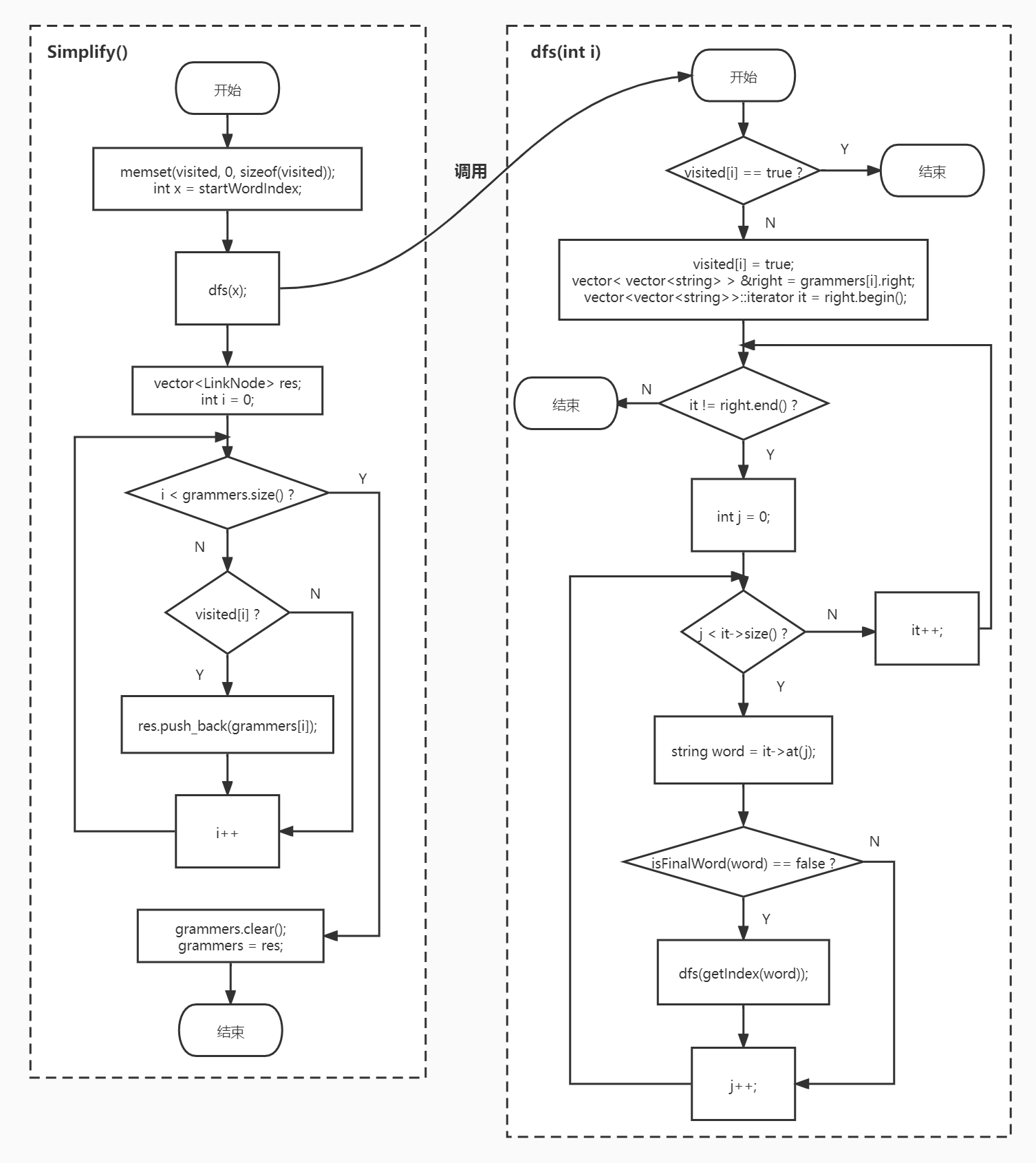
去除多余规则

# 去除左递归

先将文法右边的非终结符号用其对应的转换规则取代，例如：S -> Qc | c，R -> Sa | a，Q -> Rb | b，就先把 S 带入 R，然后把 R 带入 Q 中，这种做法可以使得间接的左递归也转化成直接左递归
然后再开始消除直接左递归，例如 A -> Aa|b，就转换成 A -> bA‘，A’ -> aA’ | ε

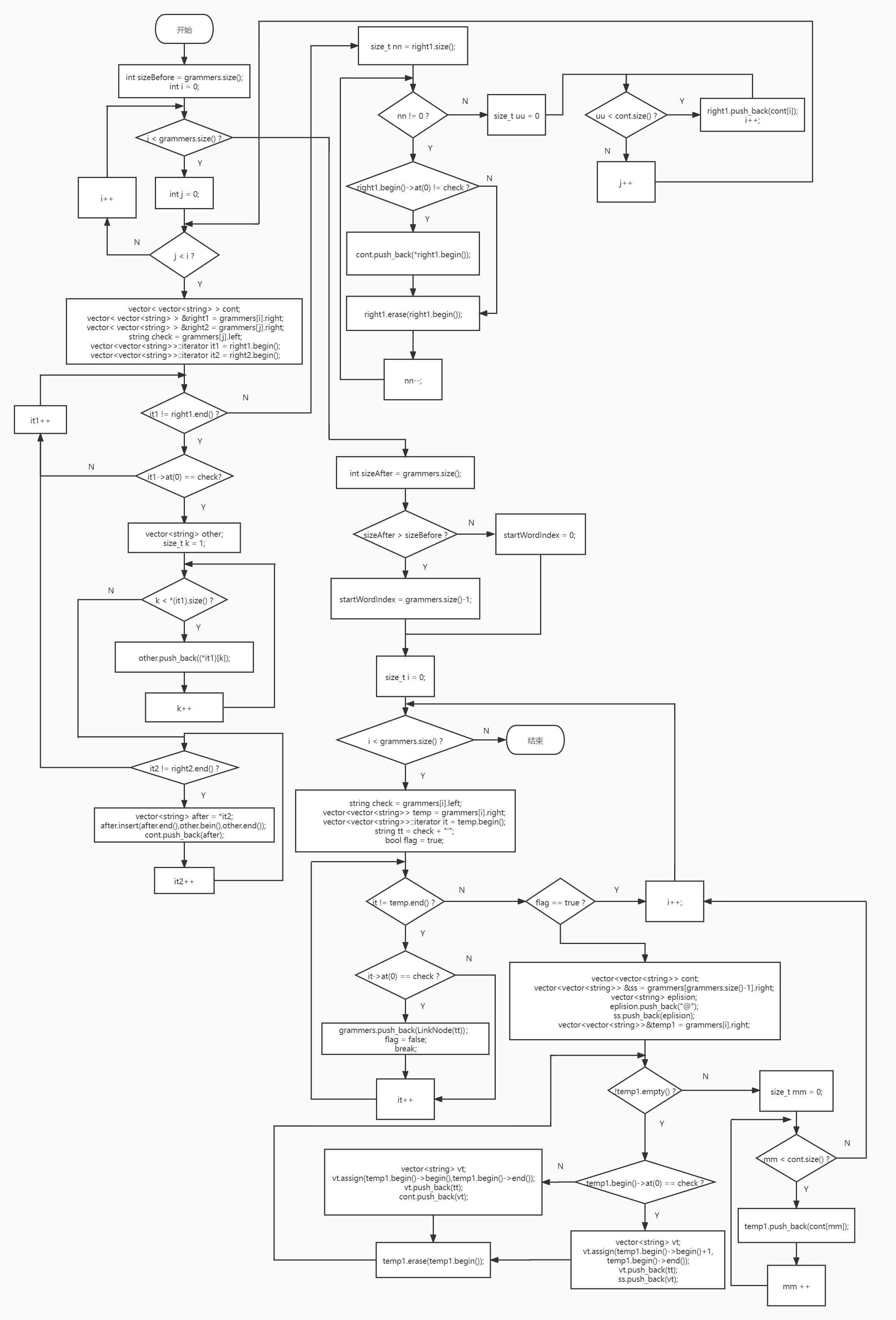
去除左递归

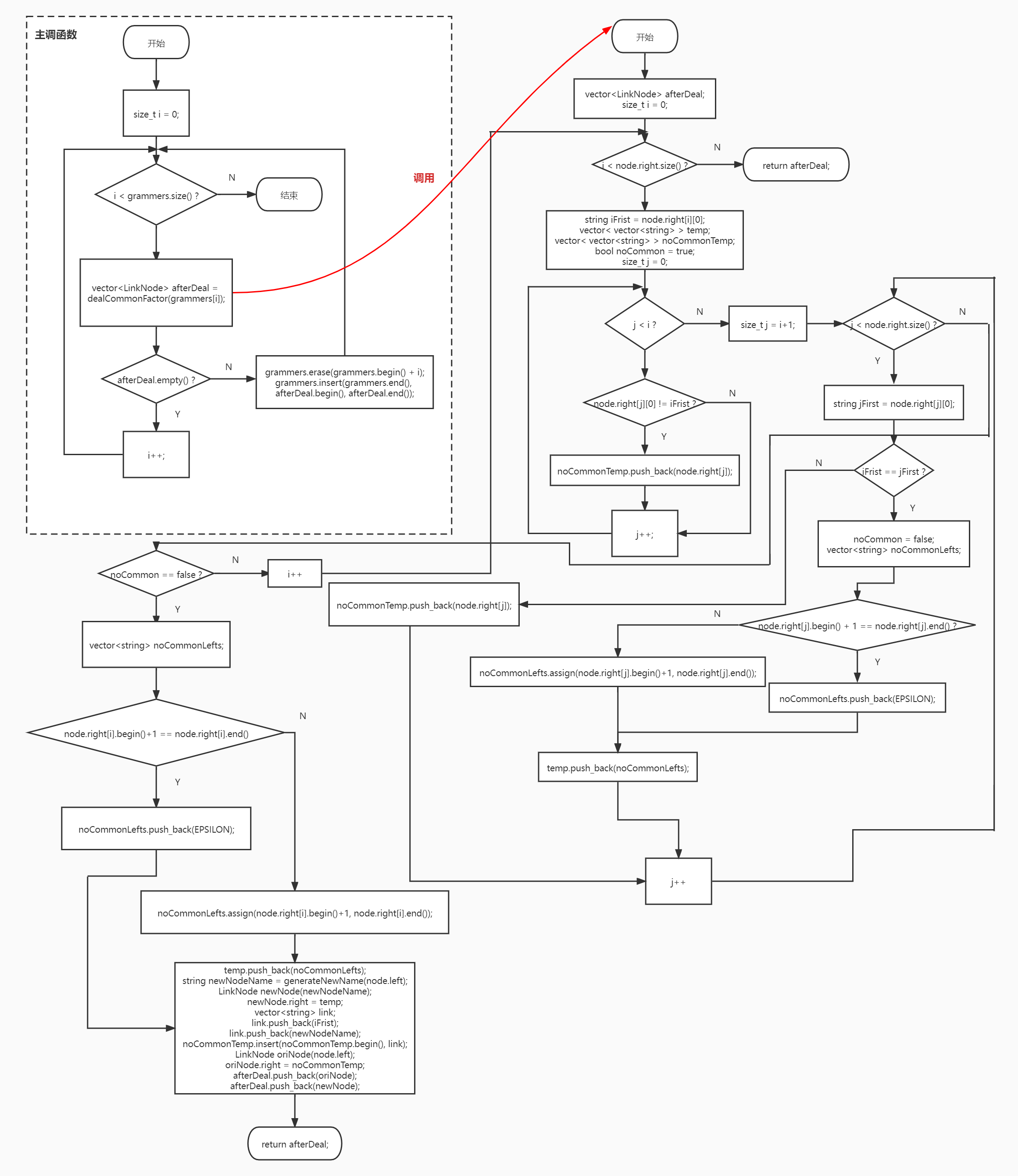
# 去除左公因子

处理的思路是每次只寻找一个左公因子

例如 A -> ab | abc
第一次处理后变成 A -> aA’，A’ -> b | bc
第二次处理后变成 A -> aA’，A‘ -> bA’’，A’‘ -> ε | c

定义从调函数，其功能是对于某条文法规则，若有左公因子，就返回处理好后的（一条变多条）文法规则，若没有左公因子，就返回一个空的 vector；定义一个主调函数，定义变量 i，当 i 小于文法数量时，就一直执行从调函数，若从调函数返回的向量为空，就说明此文法规则无左公因子，那么 i++，否则就将目前处理的文法规则替换为从调函数返回的（多条）文法规则

因为逻辑比较复杂，所以流程图化的有点乱

提取左公因子

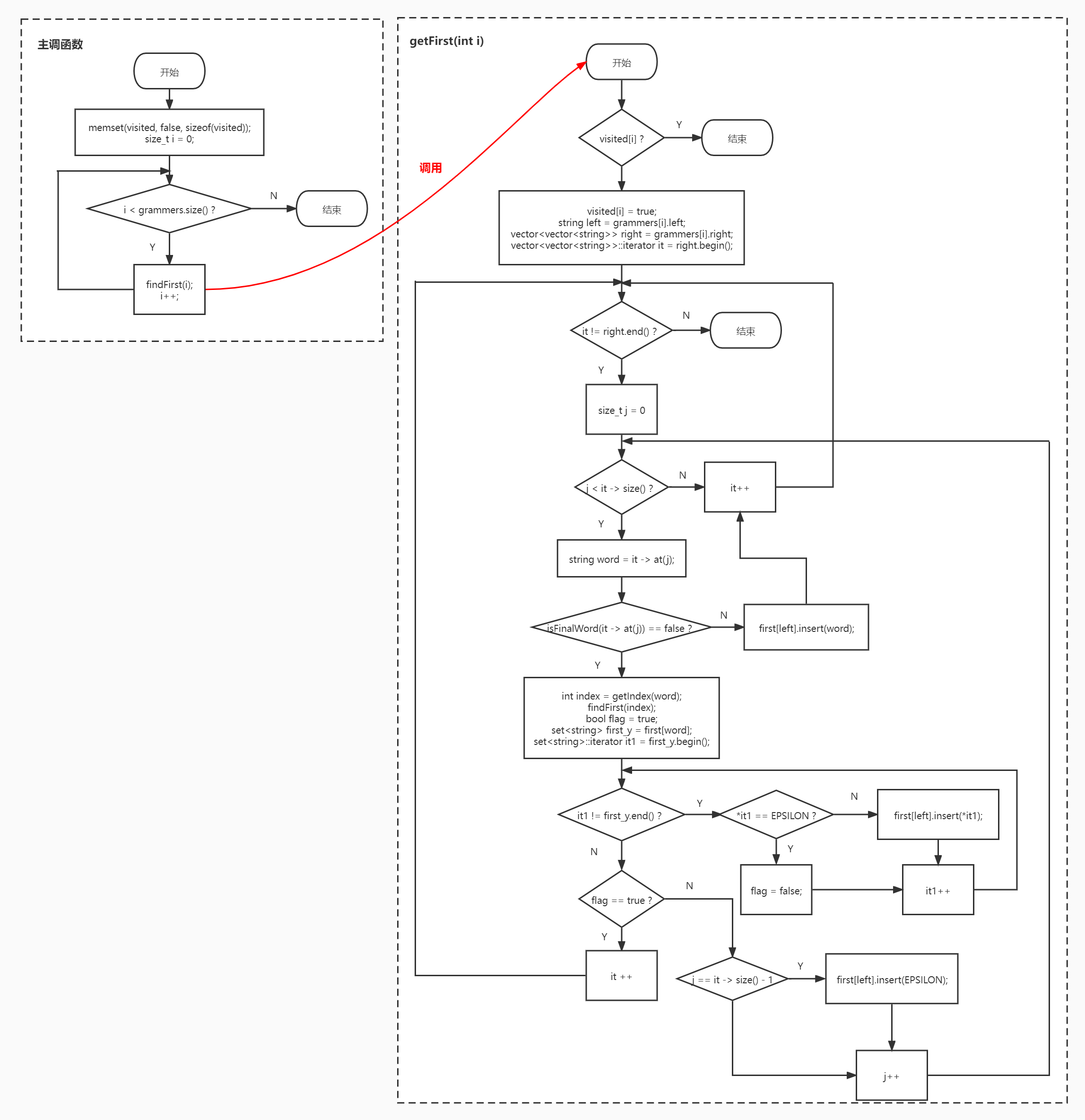
# 求 first 集合

对于规则 X -> x1x2…xn，first (x) 的计算方法如下：

first(X) = {}
k = 1
while(k <= n)
{
	if(xk为终结符号或ε)
        first(xk) = xk;
    first(x) = first(x) ∪ first(xk) - {ε};
    if(ε 不属于 first(xk))
        break;
    k++;
} 
if(k == n + 1)
    first(x) += {ε};

求first集合

# 求 follow 集合

计算 follow 集合的算法如下：

follow(开始符号) = {$}
其他任何一个非终结符号A，则执行follow(A) = {}
while(有follow集合在变化)
    循环：对每条文法规则A -> X1X2...Xn都执行
    	对于每个非终结符号Xi，都执行
    		把first(Xi+1Xi+2...Xn)-{ε}添加到follow(Xi)
    		if(ε in first(Xi+1Xi+2...Xn))
                把follow(A)添加到follow(Xi)